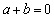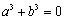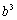对于结论：当时，也成立．若将a看成的立方根，将b看成的立方根，由此得出这样的结论：“如果两数的立方根互为相反数，那么这两个数也互为相反数”．
（1）举一个具体的例子来判断上述结论是否成立；
（2）若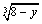和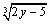互为相反数，且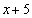的平方根是它的本身，求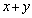的立方根．

答案

（1）如，则，即2与
互为相反数，所以“如果两数的立方根互为相反数，那么这两个数也互为相反数”结论成立；
（2）的立方根是．

知识点：相反数  平方根  立方根  

解：（1）如+=0，则2+（﹣2）=0，即2与﹣2互为相反数；
所以“如果两数的立方根互为相反数，那么这两个数也互为相反数”成立；
（2）∵和互为相反数，
∴+=0，
∴8﹣y+2y﹣5=0，
解得：y=﹣3，
∵x+5的平方根是它本身，
∵x+5=0，
∴x=﹣5，
∴x+y=﹣3﹣5=﹣8，
∴x+y的立方根是﹣2．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>