如图,BE,BD是△ABC中∠ABC的内、外角平分线,AD⊥BD于D,AE⊥BE于E,交BC的延长线于F.
(1)判断四边形ADBE的形状,并说明理由.
(2)连接DE,DE与BF相等吗?为什么?
(3)当△ABC满足什么条件时,四边形ADBE是一个正方形?并给出证明.

答案
(1)四边形ADBE是矩形,理由略;
(2)相等,理由略;
(3)△ABC是等腰直角三角形时,四边形ADBE是一个正方形,证明略.
知识点:特殊平行四边形的性质和判定
解:(1)四边形![]() 是矩形;
是矩形;
理由:∵![]() ,
,![]() 是
是![]() 中
中![]() 的内、外角平分线,
的内、外角平分线,
∴![]() ,
,
∵![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∴![]() ,
,
则![]() ,
,
∴四边形![]() 是矩形.
是矩形.
(2)![]() ,
,
理由:在![]() 和
和![]() 中,
中,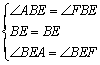 ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() .
.
(3)![]() 为直角三角形时,四边形
为直角三角形时,四边形![]() 是一个正方形,
是一个正方形,
理由:∵四边形![]() 是矩形,
是矩形,
∴当![]() 时,四边形
时,四边形![]() 是一个正方形,
是一个正方形,
∴![]() 为直角三角形时,
为直角三角形时,![]() ,
,
则![]() ,
,![]() ,
,
故![]() ,
,
∴矩形![]() 是正方形.
是正方形.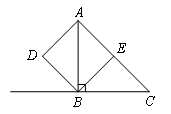
略








