如图,△ABC和△CDE都是正三角形,且∠EBD=62°,则∠AEB的度数是( )
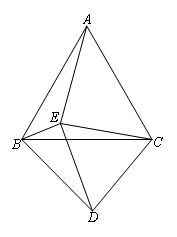
- A.124°
- B.122°
- C.120°
- D.118°
答案
正确答案:B
知识点:略
如图,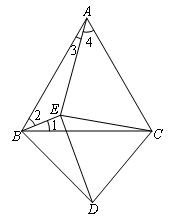
∵△ABC和△CDE都是正三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠BCD=∠ACE,
∴△ACE≌△BCD(SAS),
∴∠DBC=∠4,
即62°-∠1=60°-∠3,
即62°-(60°-∠2)=60°-∠3,
∴∠2+∠3=58°,
在△ABE中,
∠AEB=180°-(∠2+∠3)=122°.
故选B.
略








