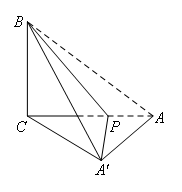
如图，在Rt△ABC中，∠ACB=90°，且AC=8，BC=6，点P是边AC上一动点，以直线BP为轴把△ABP折叠，使得点A落在图中点A′处，连接AA′，A′C，当△AA′C是直角三角形时，则线段CP的长是____.

分析：直角顶点不确定，需要分类讨论．作出精准图形，根据折叠的性质转移边长和角度求解．
解答：在Rt△ABC中，由勾股定理得AB=10，
由折叠可得，PA=PA′，
∴点A′在以B为圆心，BA长为半径的圆上，
需要注意，点P在线段AC上，点A′的轨迹实际是这个圆的一部分．
①当时，
在△PAA′中，PA=PA′，
∴不可能等于90°，这种情况不成立．
②当时，
由直径所对的圆周角是90°可得，此时点A′在以AC为直径的圆上，
如图，

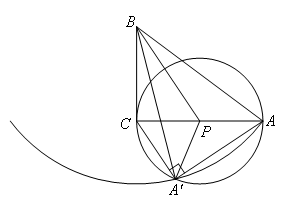
∵，PA=PA′，
∴，
∵，
∴，
∴．
③当时，
如图，此时点A′在BC延长线上，

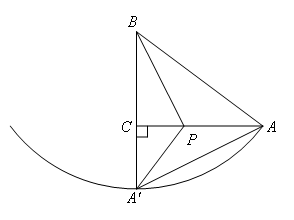
由折叠得，，，
∴，
在Rt△A′CP中，，
∴．
综上，线段CP的长是3或4．

略