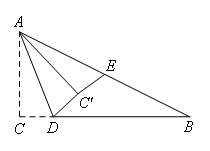
如图，在△ABC中，∠ACB=90°，AC=2，BC=4，E为边AB的中点，点D是BC边上的动点，把△ACD沿AD翻折，点C落在C′处，若△AC′E是直角三角形，则CD的长为____.

分析：折叠过程中AC′=AC=2，则点C′轨迹是圆（因为D在BC上运动，应该是一段弧）；再结合直角三角形存在性，分别以三个顶点为直角顶点进行讨论即可．
首先作出运动轨迹图：

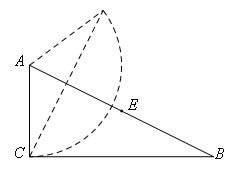
①若A为直角顶点，则AC′⊥AE，如图所示：

不存在；
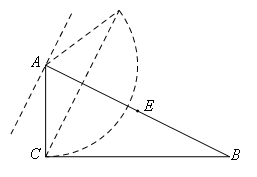
②若E为直角顶点，则C′E⊥EA，如图所示：

不存在；
③若点C′为直角顶点，则点C′在以AE为直径的圆上，如图所示：

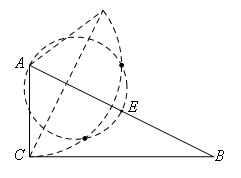
故两条轨迹的交点即为所求C′（共两个），
交点在AB上方的情况，如图所示：

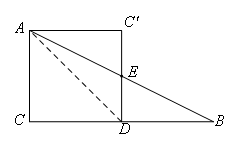
由于AC′=AC=2，AE=，
可得∠EAC′=∠B，故∠CAC′=90°，此时四边形ACDC′为正方形，
易得CD=CA=2；
交点在AB下方的情况，如图所示：

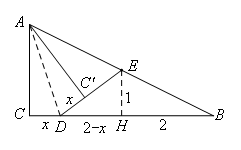
由上可得△EAC′三边长为1，2，，
则Rt△DEH中，由勾股定理得：
，解得．
综上，CD长为．

略