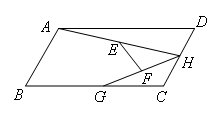
如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H,G分别是边CD,BC上的动点.连接AH,HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )
- A.1
- B.
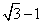
- C.
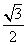
- D.
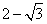
答案
正确答案:C
知识点:略
如图,连接AG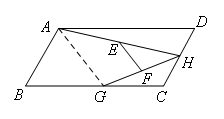
∵点E为AH的中点,点F为GH的中点
∴EF∥AG且EF=![]() AG
AG
∵点G是边BC上的动点
当点G与C点重合时,AG的长最大,即为对角线AC的长
∵∠C=120°,AD=2AB=4
∴∠B=60°
∴△ABC是直角三角形,AGmax=![]()
∴EFmax=![]() AGmax=
AGmax=![]()
当AG⊥BC时,AG的长最小
此时△ABG是直角三角形
∵∠B=60°,AB=2
∴AGmin=![]()
∴EFmin=![]() AGmin=
AGmin=![]()
∴EFmax-EFmin=![]()
故选C
略








