已知:如图,在四边形ABCD中,AB=CD,AB∥CD,E,F分别是DA,BC延长线上的点,且AE=CF,连接EF交BD于点O.
求证:△EOD≌△FOB
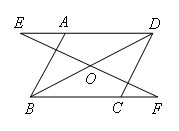
证明:如图,
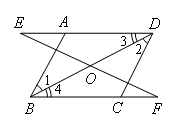
∵AB∥DC
∴∠1=∠2
在△ABD和△CDB中
∴△ABD≌△CDB( )
∴
∵AE=CF
∴AE+AD=CF+CB
即ED=FB
在△EOD和△FOB中
∴△EOD≌△FOB(AAS)
① ;②
;② ;③SAS;④SSA;⑤AAS;
;③SAS;④SSA;⑤AAS;
⑥ ;
;
⑦ ;⑧
;⑧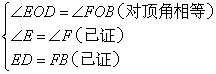 ;
;
⑨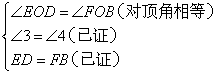 .
.
以上空缺处依次填写正确的是( )
- A.①⑤⑥⑨
- B.②③⑦⑧
- C.②④⑦⑧
- D.②③⑥⑨
答案
正确答案:D
要证△EOD≌△FOB,
已知对顶角∠EOD=∠FOB,还需要准备两组条件;
题中给出AB=CD,
由AB∥CD,可以得到∠1=∠2,BD是公共边,
进而可以证得△ABD≌△CDB(SAS),
由全等三角形对应边相等可得AD=CB,
由全等三角形对应角相等可得∠3=∠4;
由AD=CB和AE=CF可得ED=FB,
进而由AAS可以证得△EOD≌△FOB.
空缺处依次所填应为②③⑥⑨.
故选D.
略









 ;②
;② ;③SAS;④SSA;⑤AAS;
;③SAS;④SSA;⑤AAS;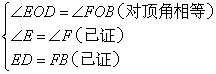 ;
;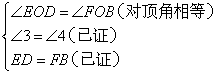 .
.