已知:如图,∠E=∠D,AM=CN,ME=ND;求证:△ABE≌△CBD
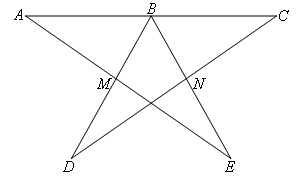
证明:如图,
在△BME和△BND中
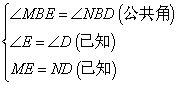
∴△BME≌△BND(AAS)
∴
∵AM=CN,ME=DN
∴AM+ME=CN+DN
即AE=CD
在△ABE和△CBD中
∴△ABE≌△CBD( )
①BE=BD(全等三角形对应边相等);②∠BME=∠BND(全等三角形对应角相等);③BM=BN(全等三角形对应边相等);④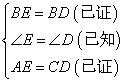 ;⑤
;⑤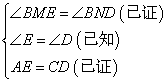 ;⑥
;⑥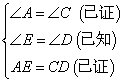 ;⑦SAS;⑧AAS.
;⑦SAS;⑧AAS.
以上空缺处依次所填正确的是( )
- A.①⑥⑧
- B.③④⑦
- C.①④⑦
- D.②⑤⑧
答案
正确答案:C
要证△ABE≌△CBD,需找三组条件,
题中只给了∠D=∠E这一组角相等,所以还要找两组条件.
观察图形,∠MBE=∠NBD,是公共角,结合已知的条件,
可得△BME≌△BND(AAS),由此得到BE=BD.
又因为AM=CN,ME=ND,
所以AM+ME=ND+CN,即AE=CD.
对比要证的结论,可以先由△BME≌△BND得BE=BD,
然后由SAS证△ABE≌△CBD.
故选C.
略








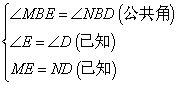
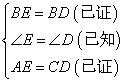 ;⑤
;⑤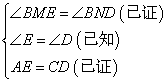 ;⑥
;⑥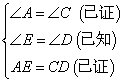 ;⑦SAS;⑧AAS.
;⑦SAS;⑧AAS.