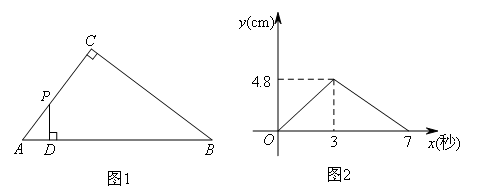
如图1，在Rt△ABC中，∠ACB=90°，点P以每秒2cm的速度从点A出发，沿折线AC—CB运动，到点B停止．过点P作PD⊥AB，垂足为D，PD的长y(cm)与点P的运动时间x(秒)的关系图象如图2所示，则下列说法错误的是( )
- A.AC=6cm
- B.△ABC的面积为48cm2
- C.BC=8cm
- D.AB=10cm
答案
正确答案：B
知识点：用图象表示变量之间的关系
关系图象上横轴表示点P运动的时间，纵轴表示PD的长，
由A到C时，y随x的增大而增大，到点C时x=3，y=4.8，
可知AC=2×3=6，△ABC的高h为4.8；
由C到B时，y随x的增大而减小，到点B时x=7，y=0，
可知BC=2×(7-3)=8；
所以S△ABC=
×AC×BC=×6×8=24，
又因为S△ABC=×AB×4.8，因此AB=10．
故选B．
略
WORD格式（