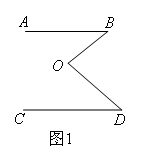
如图所示,AB∥CD,BO与DO相交于点O,从图1中可以得出,∠O=∠B+∠D,那么图2和图3针对三个角关系的结论正确的是( )
- A.图2:∠O=∠B+∠D;图3:∠O=∠B+∠D
- B.图2:∠O=∠B+∠D;图3:∠D=∠O+∠B
- C.图2:∠O+∠B+∠D=360°;图3:∠O=∠B+∠D
- D.图2:∠O+∠B+∠D=360°;图3:∠D=∠O+∠B
答案
正确答案:D
知识点:平行线的性质
从已知出发,由AB∥CD,要找同位角、内错角和同旁内角,
因此要找截线或构造平行线.
对图1:如图,过点O作OE∥AB,因为CD∥AB,
根据平行于同一条直线的两条直线互相平行,得OE∥CD∥AB,
根据平行线的性质,得∠B=∠1,∠2=∠D,
所以∠BOD=∠1+∠2=∠B+∠D.
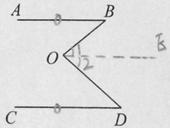
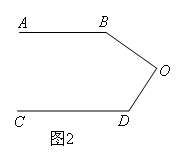
对图2:如图,
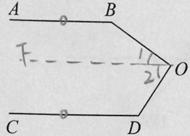
过点O作OF∥AB,因为CD∥AB,
根据平行于同一条直线的两条直线互相平行,得OF∥CD∥AB,
根据平行线的性质,得∠B+∠1=180°,∠2+∠D=180°,
所以∠B+∠1+∠2+∠D=∠B+∠BOD+∠D=360°.
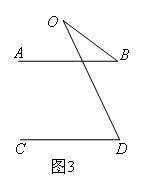
对图3:如图,
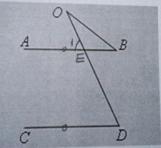
由AB∥CD,得∠D=∠1,因为∠1是△OBE的一个外角,
根据外角定理,得∠1=∠O+∠B,等量代换得∠D=∠O+∠B.
故选D.
略










