已知:如图,点E,F分别在AB,CD上,AF⊥CE,垂足为点O,∠1=∠B,∠A+∠2=90°.
求证:AB∥CD.
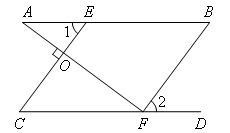
证明:如图,
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行)
请你仔细观察下列序号所代表的内容:
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
③∵AF⊥CE(已知)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
横线处应填写的过程,顺序正确的是( )
- A.⑤③①②④
- B.③④①②⑤
- C.⑤④③①②
- D.⑤②④
答案
正确答案:A
知识点:平行线的判定 平行线的性质 同角或等角的余角相等
要证AB∥CD,要找同位角、内错角或同旁内角.
根据题中的条件,由∠1=∠B得CE∥BF.
又因为EC⊥AF,可得∠AOE=90°,结合CE∥BF,可得∠AFB=90°.
再由∠CFD是一个平角,得∠AFC+∠2=90°.
又因为∠A+∠2=90°,由同角或等角的余角相等,得∠AFC=∠A.
最后,由内错角相等,两直线平行,得AB∥CD.
故选A.
略








