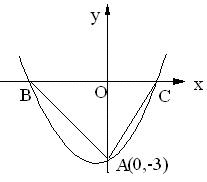
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于A点.
(1)根据图象确定a,b,c的符号;
(2)如果点A的坐标为(0,-3),∠ABC=45°, ∠ACB=60°,求这个二次函数的解析式.
答案
(1)∵抛物线开口向上且对称轴在y轴左侧,∴a>0且a、b同号,即b>0
又抛物线与y轴交点纵坐标为负,∴c<0
(2)∵点A的坐标为(0,-3),∠ABC=45°, ∠ACB=60°
∴OB=3,OC=
∴B(-3,0)、C(,0)
设二次函数解析式为y=ax2+bx+c,将A、B、C三点的坐标代入可得,
知识点:二次函数的图象 二次函数的性质 二次函数图象与系数的关系 二次函数的应用
根据抛物线开口方向、与y轴的交点和对称轴可确定a、b、c的符号;根据题中条件可确定B、C两点的坐标,进而可求出二次函数的解析式.
计算错误








