如图,在四边形ABCD中,AD∥BC,AD<BC,∠ABC=90°,且AB=3,点E是边AB上的动点,当△ADE,△BCE,△CDE两两相似时,则AE=( )

- A.

- B.
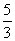
- C.
 或
或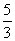
- D.
 或1
或1
答案
正确答案:D
知识点:略
①当∠CED=90°时,如图1
过点E作EF⊥CD于点F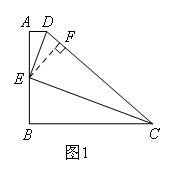
∵AD∥BC,AD<BC
∴AB与CD不平行
∴当△ADE,△BCE,△CDE两两相似时
∴∠BEC=∠CDE=∠ADE
∵∠A=∠B=∠CED=90°
∴∠BCE=∠DCE
∴AE=EF,EF=BE
∴AE=BE=![]()
②当∠CDE=90°时,如图2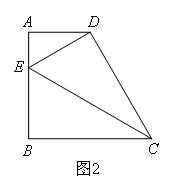
∵△ADE,△BCE,△CDE两两相似
∴∠BEC=∠CED=∠AED=60°
∴∠BCE=∠DCE=30°
∵∠A=∠B=90°
∴BE=ED=2AE
∵AB=3
∴AE=1
综上,AE的值为![]() 或1
或1
略








