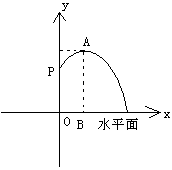
某市人民广场上要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流（在各个方向上）沿形状相同的抛物线路径落下（如图所示）．若已知OP＝3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米．
（1）求这条抛物线的解析式；
（2）若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外．

（1）根据题意可设解析式为顶点式形式，由A、P两点坐标求解析式；即设这条抛物线解析式为y=a（x＋m）²＋k，,由顶点A的坐标（1，4）知，m＝－1，k＝4，由点P的坐标（0，3）知：3=a（0-1）2+4，所以a＝－1．
所以这条抛物线的解析式为y=－（x－1）²+4．
（2）求水池半径即时求当y=0时x的值．令y=0，则0=－（x－1）²＋4，解得x₁＝3，x₂＝－1
所以若不计其它因素，水池的半径至少3米，才能使喷出的水流不至于落在池外．

不能根据实际的情况灵活设抛物线的解析式．