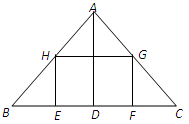
已知：在△ABC中，BC=20，高AD=16，内接矩形EFGH的顶点E、F在BC上，G、H 分别在AC、AB上，求内接矩形EFGH的最大面积．

将矩形EFGH的边长表示出来，设AD与HG的交点为P点，如图：

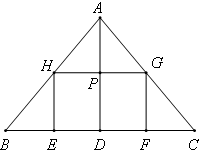
设AP长为x，因为HG∥BC，因此△AHG∽△ABC，△AHP∽△ABD，所以很容易证明
AP：AD=HG：BC HG=， 又PD=AD－AP=16－x， 所以矩形面积S=(16-x)
=－+20x
所以当x=8时，可取得最大值，最大值为80，所以内接矩形EFGH的最大面积为80.

不能将题中的几何问题转化为二次函数的最值问题