如图，直角三角形ABC的内切圆⊙E分别与AB，BC相切于点D，点F，根据图中标示的长度与角度，则线段AD的长度为( )
- A.
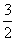
- B.
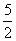
- C.
- D.
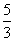
答案
正确答案：D
知识点：略
如图，记⊙E与AC相切于点G，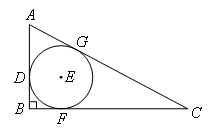
由切线长定理可得，AD=AG，BD=BF=1，CF=CG=4，
设AD=AG=x，
则AB=AD+BD=x+1，BC=BF+CF=5，AC=AG+CG=x+4，
在Rt△ABC中，∠B=90°，
由勾股定理得，(x+1)2+52=(x+4)2，
解得x=，
∴AD=．
略
WORD格式（
正确答案：D
知识点：略
如图，记⊙E与AC相切于点G，
由切线长定理可得，AD=AG，BD=BF=1，CF=CG=4，
设AD=AG=x，
则AB=AD+BD=x+1，BC=BF+CF=5，AC=AG+CG=x+4，
在Rt△ABC中，∠B=90°，
由勾股定理得，(x+1)2+52=(x+4)2，
解得x=，
∴AD=．
略