如图，直线AB，CD，BC分别与⊙O相切于E，F，G，且AB∥CD，若OB=6，OC=8，则BE+CG的长等于(    )

如图，连接OE，OF，OG，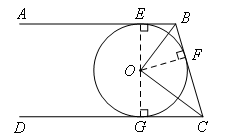

∵直线AB，BC，CD分别与⊙O相切于E，F，G，
∴OE=OF=OG，∠OEB=∠OFB=∠OGC=90°，
由切线长定理可得，BE=BF，CG=CF，
∠EOB=∠FOB，∠FOC=∠GOC，
∴BE+CG=BF+CF=BC．
由AB∥CD，∠OEB=∠OGC=90°，易证点O，E，G共线，
∴∠EOG=180°，
∴∠EOB+∠GOC=∠FOB+∠FOC=90°，
∴∠BOC=90°．
在Rt△OBC中，∠BOC=90°，OB=6，OC=8，
由勾股定理得，BC=10，
∴BE+CG=BC=10．

略