如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
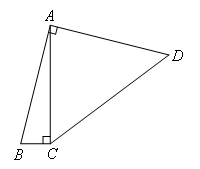
- A.
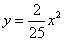
- B.
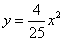
- C.
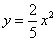
- D.
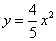
答案
正确答案:C
知识点:略
等线段共端点考虑旋转.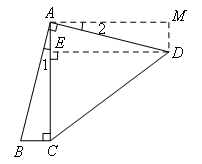
如图,过点A作AM⊥AC于点A,且使得AM=AC,连接MD,
过点D作DE⊥AC于点E.
∵∠BAD=90°,AM⊥AC
∴∠1+∠CAD=90°,∠2+∠CAD=90°
∴∠1=∠2
∵AB=AD,AM=AC
∴△ABC≌△ADM(SAS)
∴∠M=∠ACB=90°,DM=BC
∴四边形AEDM为矩形,四边形DMAC为直角梯形
∴AM=DE
∵AC=4BC,若设BC=a
则DM=AE=a,AM=AC=4a,
∴CE=AC-AE=4a-a=3a
在Rt△CED中,由勾股定理得
DE2+CE2=CD2即(4a)2+(3a)2=x2
∴![]()
∴![]()
略








