在△ABC中，AB=26，AC=25，BC边上的高AD=24，则另一边BC等于(    )

由题意，有如下两种情况，△ABC为锐角三角形或钝角三角形
①如图，△ABC为锐角三角形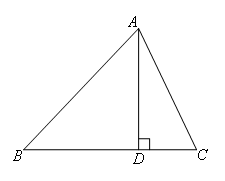

∵AD⊥BC
∴在Rt△ABD中，∠ADB=90°，AB=26，AD=24
由勾股定理得，BD=10
同理，在Rt△ADC中，∠ADC=90°，AD=24，AC=25
由勾股定理得，CD=7
∴BC=BD+CD=10+7=17
②如图，△ABC为钝角三角形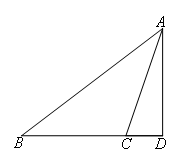

∵AD⊥BC
∴在Rt△ABD中，∠ADB=90°，AB=26，AD=24
由勾股定理得，BD=10
同理，在Rt△ADC中，∠ADC=90°，AD=24，AC=25
由勾股定理得，CD=7
∴BC=BD-CD=10-7=3
综上，BC的长为3或17
故选A

略