已知:如图,点E在△ABC的外部,点D在BC边上,DE交AC于F,∠1=∠2=∠3,AC=AE.
求证:△ABC≌△ADE.
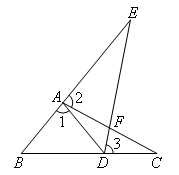
证明:如图,
∵∠1=∠2
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
∵∠3+∠C+∠DFC=∠2+∠E+∠AFE=180°
∠DFC=∠AFE,∠3=∠2
∴
在△ABC和△ADE中
∴
①∠AFE=∠DFC;②∠C=∠E;③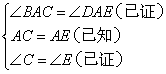 ;④
;④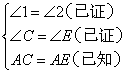 ;
;
⑤△ABC≌△ADE(AAS);⑥△ABC≌△ADE(ASA).
以上空缺处依次填写最恰当的是( )
- A.①③⑤
- B.②③⑥
- C.②④⑥
- D.②④⑤
答案
正确答案:B
知识点:全等三角形的判定
要证△ABC和△ADE全等,需要找三组条件,题中给出AC=AE,
还需要再找两组条件,考虑利用题中给出的三个相等的角,
由∠1=∠2可得∠BAC=∠DAE,
由∠3=∠2以及∠DFC=∠AFE可得∠C=∠E,
因此由ASA可以证得两个三角形全等,需要注意对应关系.
因此空缺处依次填写最恰当的是②③⑥.
故选B.
略








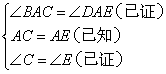 ;④
;④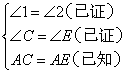 ;
;