已知：如图，在四边形ABCD中，∠A=20°，∠B=40°，∠C=30°．求∠ADC的度数．

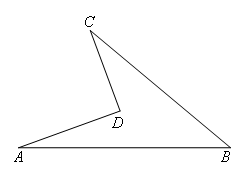
解：如图，延长AD交BC于点E．

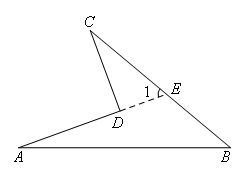
∵∠1是△ABE的一个外角（外角的定义）
∴∠1=∠A+∠B（三角形的一个外角等于和它不相邻的两个内角的和）
                           
以上空缺处所填正确的是(    )

• A.∵∠A=20°，∠B=40°（已知）
  ∴∠1=20°+40°=60°（等量代换）
  ∵∠C=30°（已知）
  ∴∠ADC=60°+30°=90°（等量代换）
• B.∵∠A=20°，∠B=40°（已知）
  ∴∠1=20°+40°=60°（等量代换）
  ∵∠ADC=∠1+∠C（外角的定义）
  ∴∠ADC=60°+30°=90°（等量代换）
• C.∵∠ADC=∠1+∠C（外角的定义）
  ∴∠ADC=∠A+∠B+∠C（三角形的一个外角等于和它不相邻的两个内角的和）
  ∴∠ADC=20°+40°+30°=90°（等量代换）
• D.∵∠ADC是△CDE的一个外角（外角的定义）
  ∴∠ADC=∠1+∠C（三角形的一个外角等于和它不相邻的两个内角的和）
  ∴∠ADC=∠A+∠B+∠C（等量代换）
  ∵∠A=20°，∠B=40°，∠C=30°（已知）
  ∴∠ADC=20°+40°+30°=90°（等量代换）

答案

正确答案：D

知识点：平行线的性质  三角形的外角  与角有关的辅助线  

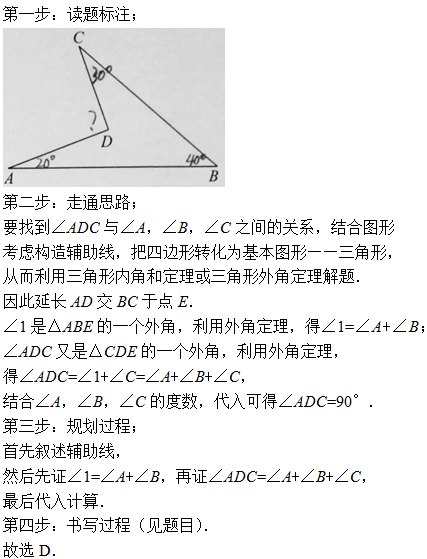
略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>