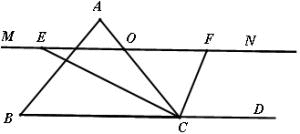
如图,△ABC中,点O是边AC上啊一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,请说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
答案
(1)OE=OF.
∵MN∥BC,∴∠OEC=∠ECB,又∵CE为∠BCO的角平分线,∴∠ECB=∠ECO,∴∠OEC=∠ECO,∴△OEC为等腰三角形,∴OE=OC,同理可证OC=OF,故OE=OF.
(2)不会是菱形.
假设在边AC上存在一点O,使四边形BCFE为菱形,则CF=FE,但∵CE为∠BCO的角平分线,CF为∠OCD的角平分线,∴∠OCE+∠OCF=90°,即△ECF为直角三角形,且∠ECF=90°,∴斜边EF>FC,与EF=FC矛盾,因此四边形BCFE不会是菱形.
(3)要使四边形AECF为正方形,只需对角线AC与EF互相垂直平分,由(1)可知,O已经是EF的中点,只需满足O为AC的中点即可保证对角线AC与EF互相平分,又∵EF是水平方向的线段,要保证AC与EF垂直,只需AC为竖直方向的线段即可,即三角形ABC为直角三角形,且∠C=90°.因此,当O运动到AC的中点,△ABC为直角三角形时,四边形AECF是正方形.
(1)可判断OE=OF.
由已知的条件MN∥BC,知∠OEC=∠ECB,又因为CE为∠BCO的角平分线,可以知道∠ECB=∠ECO,∠OEC=∠ECO,所以△OEC为等腰三角形,则OE=OC,同理可以证明OC=OF,因此OE=OF.
(2)不会是菱形.
我们可以假设在边AC上存在一点O,使四边形BCFE为菱形,则CF=FE,但因为CE为∠BCO的角平分线,CF为∠OCD的角平分线,所以∠OCE+∠OCF=90°,即△ECF为直角三角形,且∠ECF=90°,所以斜边EF>FC,这就与EF=FC矛盾,因此四边形BCFE不会是菱形.
(3)要使四边形AECF为正方形,根据正方形的判定定理可以知道,只需对角线AC与EF互相垂直平分,由(1)可知,O已经是EF的中点,只需满足O为AC的中点即可保证对角线AC与EF互相平分,又∵EF是水平方向的线段,要保证AC与EF垂直,只需AC为竖直方向的线段即可,这样三角形ABC就为直角三角形,且∠C=90°.因此,当O运动到AC的中点,△ABC为直角三角形时,四边形AECF是正方形.
略








