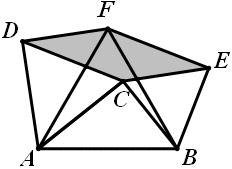
在直角三角形ABC中,∠C=90°,AB=5,AC=4,分别以△ABC三边为边作等边三角形(如图所示),求四边形DCEF的面积.
答案
∵BC=BE=3,BA=BF=5,且∠ABC+∠CBF=60°,∠CBF+∠FBE=60°,∴∠ABC=∠FBE,∴△ABC≌△FBE(SAS),∴∠BEF=90°,EF=4,同理可证△AFD≌△ABC,∴DF=3,∵∠FDA=90°,∠CDA=60°,∴∠FDC=30°,由两次三角形的全等可以知道,△AFD≌△FBE,∴∠DFA+∠EFB=90°,∴∠DFE=150°,∴∠DFE与∠FDC是互补的,∴四边形DCEF为平行四边形,又∵DF=3,∠FDC=30°,∴四边形DCEF的边DC上的高为,∴四边形DCEF的面积S=4×
=6.
知识点:平行四边形的判定
思路1:由已知条件可知,BC=BE=3,BA=BF=5,又因为∠ABC+∠CBF=60°,∠CBF+∠FBE=60°,所以∠ABC=∠FBE,因此可证△ABC≌△FBE,所以∠BEF=90°,所以EF=4,同理可证△AFD≌△ABC,因此DF=3,由∠FDA=90°,∠CDA=60°,可以知道∠FDC=30°,由两次三角形的全等可以知道,△AFD≌△FBE,因此∠DFA+∠EFB=90°,故∠DFE=150°,所以∠DFE与∠FDC是互补的,因此四边形DCEF为平行四边形,由各边的长及∠FDC=30°,可容易计算出来四边形DCEF的边DC上的高为,所以四边形DCEF的面积S=4×
=6.
思路2:最后再求面积的时候,可以根据分割的思想进行求解,即四边形DCEF的面积=△AFD的面积+△ABF的面积+△FBE的面积-(△ACD的面积+△ABC的面积+△BCE的面积),其中要求的三角形都是特殊的三角形,易计算,答案为:6.
不能很好的利用全等三角形的性质及直角三角形的性质进行解题.








