八年级数学上学期期末考试预测卷一（人教版）-八年级试卷-众享学科测评

学科测评首页

八年级数学上学期期末考试预测卷一（人教版）

满分100分答题时间90分钟

已经有1102位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 下列运算结果正确的是()

2.(本小题3分) 下列说法正确的有() ①无理数是无限小数;②不带根号的数一定是有理数;③两个无理数的和一定是无理数;④负数没有立方根;⑤的平方根是±8.

3.(本小题3分) 如图,,,增加下列条件:①②;③;④.其中能使的条件有()

4.(本小题3分) 动手操作:将如图1中的正方形纸片沿其中一条对角线对折后,再沿原正方形的另一条对角线对折,如图2所示,最后将图2剪下一部分纸片,如图3所示,若下列有一图形为图3的展开图,则此图为()

5.(本小题3分) 如图,直线与直线的图象相交于点P(-2,-5),则下列结论正确的是()

6.(本小题3分) 小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是()

解答题(本大题共小题，共分)

7.(本小题3分) 如图，在△ABC中，∠C=90°，CD=5.按以下步骤作图：①以点A为圆心，小于AC的长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于的长为半径画弧，两弧相交于点G；③作射线AG交BC边于点D.点P为AB边上的动点，则DP的最小值为 .

8.(本小题3分) 的整数部分是a，小数部分是b，则= .

9.(本小题3分) 若等腰三角形的一个内角是另一个内角的2倍，则等腰三角形的顶角为 .

10.(本小题3分) 若多项式x²+(m-2)x+4能用完全平方公式分解因式，则m的值是 .

11.(本小题3分) 如图，在△ABC中，AB=AC，∠B=30°，AB的垂直平分线EF交AB于点E，交BC于点F，EF=2cm，则BC的长为 .

12.(本小题3分) △ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP= .

13.(本小题3分) 如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A，B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.若E为边OA上的一个动点，当△CDE的周长最小时，点E的坐标为 .

14.(本小题3分) 如图，已知直线l₁：y=与直线l₂：y=-2x+16相交于点C，直线l₁，l₂分别交x轴于A，B两点，矩形DEFG的顶点D，E分别在l₁，l₂上，顶点F，G都在x轴上，且点G与点B重合， 那么S_矩形_DEFG：S_△_ABC= .

15.(本小题3分) 如图，甲类纸片是边长为2的正方形，乙类纸片是边长为1的正方形，丙类纸片是长、宽边长分别是2和1的长方形.现有甲类纸片1张，乙类纸片4张，则应至少取丙类纸片张才能用它们拼成一个新的正方形.

16.(本小题6分) （1） （2）

17.(本小题6分) 先化简，再求值：，其中a，b满足

18.(本小题6分) 如图，在△ABC中，AB=AC，点D，E在BC边上，且AD=AE.求证：BD=CE.

19.(本小题8分) 如图，在平面直角坐标系中，直线l经过点A（0，4）和B（-2，0）两点.（1）求直线l的表达式；（2）若C（4，2），D（m，0），且△ABO与△OCD全等，①则m的值为（直接写出结论）；②若直线l向下平移n个单位后经过点D，求n的值.

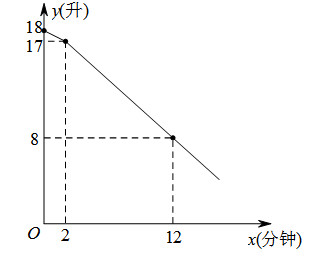
20.(本小题9分) 教室里放有一台饮水机，饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒，每个同学所接的水量都是相等的.两个放水管同时打开时，他们的流量相同.放水时先打开一个水管，过一会儿，再打开第二个水管，放水过程中阀门一直开着.饮水机的存水量y（升）与放水时间x（分钟）的函数关系如图所示：（1）求饮水机的存水量y（升）与放水时间x（分钟）（x≥2）的函数关系式.（2）如果打开第一个水管后，2分钟时恰好有4个同学接水结束，则前22个同学接水结束共需要几分钟？（3）按（2）的放法，在课间10分钟内班级中最多有多少个同学能及时接完水？

21.(本小题9分) 如图，梯形ABCD中，AD∥BC，CE⊥AB，△BDC为等腰直角三角形，CE与BD交于点F，连接AF，G为BC中点，连接DG交CF于点M.证明：（1）CM=AB；（2）CF=AB+AF.

22.(本小题11分) 如图，直线与x轴、y轴分别交于A，B两点，点C的坐标为（-3，0），P（x，y）是直线上的一个动点（点P不与点A重合）.（1）在P点运动过程中，试写出△OPC的面积S与x的函数关系式；（2）当P运动到什么位置时，△OPC的面积为，求出此时点P的坐标；（3）过P作AB的垂线分别交x轴、y轴于E，F两点，是否存在这样的点P，使△EOF≌△BOA？若存在，求出点P的坐标；若不存在，请说明理由.