九年级十一短训班动点存在性问题学力练习
满分100分 答题时间30分钟
已经有141位用户完成了练习
单选题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
2.(本小题50分)
(2010浙江舟山)如图,在菱形ABCD中,AB=2cm,∠BAD=60°,E为CD边中点,点P从点A开始沿AC方向以每秒
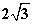 cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒(1)当点P在线段AO上运动时.①请用含x的代数式表示OP的长度;②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围);(2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.
cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒(1)当点P在线段AO上运动时.①请用含x的代数式表示OP的长度;②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围);(2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.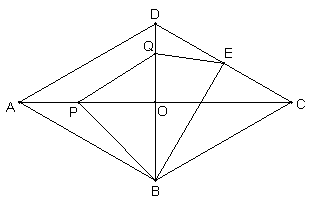
核心考点: 菱形的判定与性质 梯形 运动变化型问题
上一讲:
下一讲:



