九年级数学四边形相关证明(证明三)拔高练习-九年级试卷-众享学科测评

学科测评首页

九年级数学四边形相关证明(证明三)拔高练习

满分120分答题时间90分钟

已经有109位用户完成了练习

本试卷为的课后练习题

证明题(本大题共小题，共分)

1.(本小题20分) （2011湖南改编）如图所示，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，顺次连接EF、FG、GH、HE． （1）请判断四边形EFGH的形状，并给予证明； （2）四边形EFGH可能是菱形，请给出判断依据； （3）四边形EFGH可能是矩形，请给出判断依据； （4）四边形EFGH可能是正方形，请给出判断依据；

2.(本小题20分) （2011四川改编）如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点. (1)当四边形ABCD的边至少满足_____条件时，四边形EFGH是菱形. (2)当四边形ABCD的边至少满足_____条件时，四边形EFGH是矩形. (3)当四边形ABCD的边至少满足_____条件时，四边形EFGH是正方形.

3.(本小题20分) （2011山东）如图，在△ABC中，点O是AC边上（端点除外）的一个动点，过点O作直线MN∥BC.设MN交∠BCA平分线于点E，交∠BCA的外角平分线于点F，连接AE、AF.那么当点O运动到何处时，四边形AECF是矩形？并证明你的结论.

探究题(本大题共小题，共分)

4.(本小题20分) （2011辽宁）如图1，在△ABC中，∠ABC=90°，AB=BC，BD为斜边AC上的中线，将△ABD绕点D顺时针旋转α（0°＜α＜180°），得到△EFD，点A的对应顶点是E，点B的对应顶点是F，连接BE、CF. （1）判断BE与CF的位置关系、数量关系，并说明理由； （2）若连接BF、CE，请直接写出在旋转过程中四边形BFEC能形成哪些特殊四边形； （3）如图2，将△ABC中AB=BC改为AB≠BC时，其他条件不变，直接写出α为多少度时（1）中的两个结论同时成立.

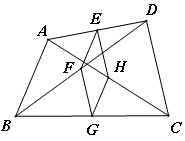
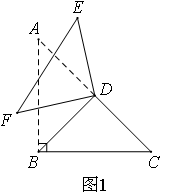
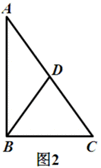
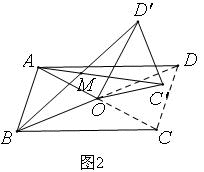
5.(本小题20分) （2011辽宁）在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠DOC=α.将△DOC绕点O按逆时针方向旋转得到△D’OC’（0°＜旋转角＜90°）.连接AC’、BD’，AC’与BD’相交于点M. （1）当四边形ABCD是矩形时，如图1，请猜想AC’与BD’的数量关系以及∠AMB与α的大小关系，并证明你的猜想； （2）当四边形ABCD是平行四边形时，如图2，已知AC=kBD，请猜想此时AC’与BD’的数量关系以及∠AMB与α的大小关系，并证明你的猜想； （3）当四边形ABCD是等腰梯形时，如图3，AD∥BC，此时（1）中AC’与BD’的数量关系是否成立？∠AMB与α的大小关系是否成立？不必证明，直接写出结论.

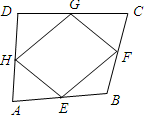
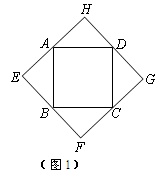
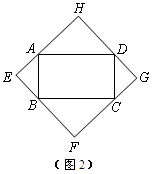
6.(本小题20分) （2011浙江）以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连结这四个点，得四边形EFGH． （1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）； （2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°）， ① 试用含α的代数式表示∠HAE； ② 求证：HE=HG； ③ 四边形EFGH是什么四边形？并说明理由

上一讲: 下一讲: