九年级数学双垂直模型之变形、应用、拓展(相似)基础练习-九年级试卷-众享学科测评

学科测评首页

九年级数学双垂直模型之变形、应用、拓展(相似)基础练习

满分100分答题时间100分钟

已经有292位用户完成了练习

本试卷为的课后练习题

填空题(本大题共小题，共分)

1.(本小题10分) 如图，梯形ABCD中，AB//DC，∠B=90°，E为BC上一点，且AE⊥ED．若BC=12，DC=7，BE：EC=1：2，则AB的长为____________．

2.(本小题10分) 如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连结OB，将纸片OABC沿OB折叠，使点A落在A'的位置上．若OB= $\footnotesize \sqrt{5}$ ， $\footnotesize \frac{BC}{OC}=\frac{1}{2}$ ，求点A'的坐标为_________．

解答题(本大题共小题，共分)

3.(本小题30分) 在平面直角坐标系xOy中，点A的坐标为（4，2），正比例函数y=kx图像与线段OA的夹角是45°，求这个正比例函数的表达式．

证明题(本大题共小题，共分)

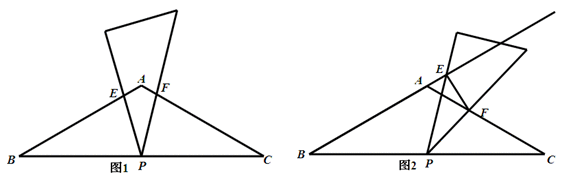
4.(本小题25分) （2）将三角板绕点P旋转到图2的情形时，三角形的两边分别交BA的延长线、边AC于点E、F．探究：①△BPE与△CFP还相似吗？②连接EF，△BPE与△PEF是否相似？并证明． 如图，等腰三角形ABC中∠BAC=120°，P为BC中点，小颖拿着含30°角的三角板，使30°角的顶点落在P点，三角板围绕点P旋转． （1）如图1，当三角板的两边分别交AB、AC于点E、F时，求证：△BPE∽△CFP； （2）将三角板绕点P旋转到图2的情形时，三角形的两边分别交BA的延长线、边AC于点E、F．探究：①△BPE与△CFP还相似吗？②连接EF，△BPE与△PEF是否相似？并证明．

5.(本小题25分) 在△ABC中，AC=BC，∠ACB=90°，点M是AC上的一点，点N是BC上的一点，沿着直线MN折叠，使得点C恰好落在边AB上的P点，求证：MC：NC=AP：PB．

上一讲: 下一讲: