2.(本小题15分) （上接第1题）（2）在探究“等对角四边形”性质时，小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．下列说法正确的是(    )

核心考点: 等腰三角形的判定与性质  类比探究问题 

4.(本小题15分) [问题情境]张老师给爱好学习的小军和小俊提出这样一个问题：如图1，在△ABC中，
AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．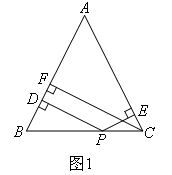

小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．
小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．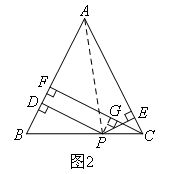

（1）[变式探究]如图3，当点P在BC延长线上时，其余条件不变，则PD，PE，CF之间的关系为(    )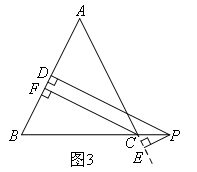

核心考点: 等腰三角形的性质  全等三角形的判定与性质  等面积法 

6.(本小题20分) （上接第4，5题）[迁移拓展]图5是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D，C，且，．M，N分别为AE，BE的中点，连接DM，CN，则△DEM与
△CEN的周长之和为(    )dm．

核心考点: 勾股定理  相似三角形的判定与性质  类比探究问题  等面积法  直角三角形斜边的中线等于斜边的一半