在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E，DF与线段AC（或AC的延长线）相交于点F．
（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；
（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F，探究线段BE，
CF，AB之间的数量关系，写出结论并说明理由；
（3）如图3，将（2）中的∠EDF绕点D顺时针旋转一定的角度，使DF与线段AC的延长线相交于点F．
作DN⊥AC于点N，若DN=FN，线段BE，CF存在什么样的数量关系？

（1）中BE的长为(    )

• A.1
• B.
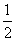
• C.
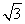
• D.

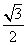
答案

正确答案：A

知识点：三角形全等性质与判定  类比探究问题  

见第6题中解析

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>