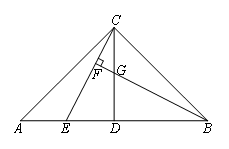
已知:如图,在△ABC中,AC=BC,∠ACB=90°,CD平分∠ACB,点E是AB边上一点.BF⊥CE于点F,交CD于点G.
求证:△ACE≌△CBG.
小明是这样想的,要证明△ACE≌△CBG,那么必须有三组条件,题目中已经给出了AC=BC,因此还需要寻找另外的两组条件,结合已知,请你选出小明要找的另外两组条件是( )
- A.∠A=∠BCG,∠ACE=∠CBG
- B.∠A=∠BCG,AE=CG
- C.∠ACE=∠CBG,AE=CG
- D.AE=CG,CE=BG
答案
正确答案:A
知识点:全等三角形的判定
分析:要证明△ACE≌△CBG,那么必须有三组条件,
题目中已经给出了AC=BC.
结合题目的条件,△ABC中,AC=BC,∠ACB=90°,
CD平分∠ACB,利用等腰三角形的性质,
得![]() ,
,![]() ,
,
且CD⊥AB,所以∠A=∠BCG;再根据∠ACB=90°,
BF⊥CE得∠ACE+∠FCB=90°,∠CBG+∠FCB=90°,
利用同角的余角相等,得∠ACE=∠CBG;
结合AC=BC,可以利用ASA判定△ACE≌△CBG.
故选A.
略








