如图,在四边形ABCD中,连接AC,添加下列各组条件,不能证明△ABC≌△CDA的是( )
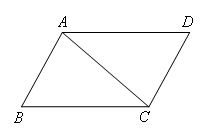
- A.AB∥CD,AB=CD
- B.AD∥BC,AD=BC
- C.BC=AD,∠B=∠D
- D.AB=CD,∠BAC=∠DCA
答案
正确答案:C
知识点:全等三角形的判定
如图,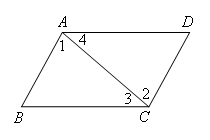
根据全等三角形判定定理,要证全等首先要找三组条件,其中必有一组边相等.
选项A中,由AB∥CD,得∠1=∠2,结合条件AB=CD,AC=CA,
可利用SAS证明两三角形全等;
选项B中,由AD∥BC,得∠3=∠4,结合条件AD=CB,AC=CA,
可利用SAS证明两三角形全等;
选项C中,有两组边对应相等,即BC=DA,AC=CA,
又有一组角相等∠B=∠D,但这组角不是两组对应边的夹角,因此不能证明两三角形全等;
选项D中,AB=CD,∠BAC=∠DCA,结合条件AC=CA,
可利用SAS证明两三角形全等.
故选C.
略








