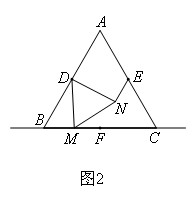
如图，已知等边三角形ABC中，点D，E，F分别为边AB，AC，BC的中点，M为直线BC上一动点，△DMN为等边三角形（点M的位置改变时，△DMN也随之整体移动）．在图1中，点M在点B左侧，在图2中，点M在线段BC上，两个图中都可以证明EN=MF．我们的思路是连接DE，DF，然后证明两个三角形全等就能解决问题，我们证明三角形全等的判定定理是(    )

• A.SSS
• B.ASA
• C.SAS
• D.SSA

答案

正确答案：C

知识点：类比探究问题  

以图1为例证明，根据题意连接DE，DF．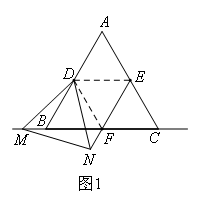

根据中位线定理可以证明：∠EDF=60°，DE=DF，
∵∠MDN=60°，
∴∠MDF=∠NDE，
∵DM=DN，
∴△MDF≌△NDE，
∴MF=NE．
通过上面的证明可以看出，
证明三角形全等使用的判定定理是SAS．
故选C

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>