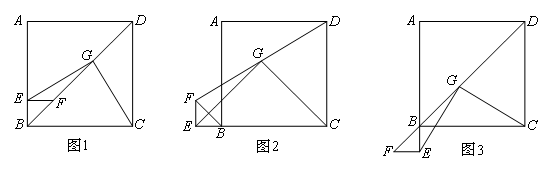
如图1,在正方形ABCD的边AB上取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG,CG,易证EG=CG且EG⊥CG.如图2,将△BEF绕点B逆时针旋转90°, 如图3,将△BEF绕点B逆时针旋转
180°,都可以得到和图1相同的结论.若不想证明三点共线,则最好作什么样的辅助线.( )
- A.
(图1)连接CE;
(图2)无需辅助线;
(图3)连接CE - B.
(图1)延长EG至点H,使GH=EG,连接DH,CE,CH;
(图2)延长EG至点H,使GH=EG,连接DH;
(图3)延长EG,交AD于点H,连接CE,CH - C.
在CD边上取一点H,使CH=BE,连接GH(适用于图1,图2,图3) - D.
(图1)延长EG,交AD的延长线于点H,连接CE,CH;
(图2)延长EG,交CD的延长线于点H;
(图3)延长EG,交AD于点H,连接CE,CH
答案
正确答案:D
知识点:类比探究问题
观察到三问都有中点,可以类比,由平行线夹中点可以类比,如图,
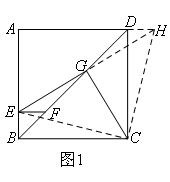
如图1,延长EG,交AD的延长线于点H,连接CE,CH.
先证明△EGF≌△HGD(AAS),得到DH=EF=BE,
再证明△BCE≌△DCH(SAS),得到CE=CH,∠BCE=∠DCH,
所以△CEH是等腰直角三角形,利用等腰直角三角形的性质即可得到EG=CG且EG⊥CG.
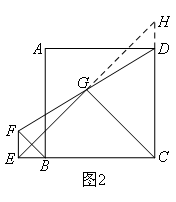
如图2,延长EG,交CD的延长线于点H.
先证明△EFG≌△HDG(AAS),得到DH=EF=BE,
所以△CEH是等腰直角三角形,利用等腰直角三角形的性质即可得到EG=CG且EG⊥CG.
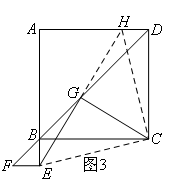
如图3,延长EG,交AD于点H,连接CE,CH.
先证明△EFG≌△HDG(AAS),得到DH=EF=BE,
再证明△BCE≌△DCH(SAS),得到CE=CH,∠BCE=∠DCH,
所以△CEH是等腰直角三角形,利用等腰直角三角形的性质即可得到EG=CG且EG⊥CG.
分析其线路图如图所示:
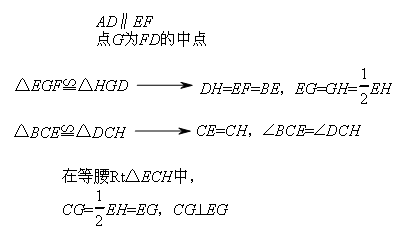
故选D.
略








