已知：如图，AB∥CD，∠1=∠2，∠E=50°，求∠F的度数．

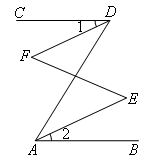
解：如图，
                           
∴DF∥AE（内错角相等，两直线平行）
∴∠E=∠F（两直线平行，内错角相等）
∵∠E=50°（已知）
∴∠F=50°（等量代换）
横线处所填最恰当的为(    )

• A.∵AB∥CD（已知）
  ∴∠FDA=∠DAE（两直线平行，内错角相等）
• B.∵AB∥CD（已知）
  ∴∠1=∠2（两直线平行，内错角相等）
  ∴∠FDA=∠DAE（等式性质）
• C.∵AB∥CD（已知）
  ∴∠CDA=∠DAB（两直线平行，内错角相等）
  ∵∠1=∠2（已知）
  ∴∠FDA=∠DAE（等式性质）
• D.∵∠1=∠2（已知）
  ∴∠FDA=∠DAE（等式性质）
  ∵AB∥CD（已知）
  ∴∠CDA=∠DAB（两直线平行，内错角相等）

答案

正确答案：C

知识点：平行线的判定  平行线的性质  

本题主要考查平行的性质与判定以及利用平行进行转移角，
先由AB∥CD得到∠CDA=∠DAB，
又由∠1=∠2进而得到∠FDA=∠DAE，
从而得到DF∥AE，再利用平行转移角可求出∠F的度数．
故选C．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>