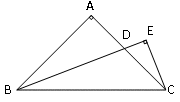
如图所示，在△ABC中，AB=AC，∠BAC=90°，BE平分∠ABC，交AC于D，CE⊥BE于E点，
求证：
答案
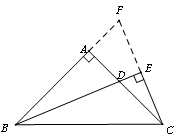
延长CE交BA的延长线于F，
∵BD平分∠ABC，BE⊥CE
∴△CBF是等腰三角形
∴E为CF的中点，即CE= CF.
∵∠BDA=∠CDE，∴∠ABD=∠ACF(等角的余角相等）
又∵∠BAD=∠CAF，AB=AC
∴△ABD≌△ACF
∴BD=CF，则CE= BD
知识点：全等三角形的判定
延长CE交BA的延长线于F，有已知条件BD平分∠ABC及BE⊥CE可知，△CBF是等腰三角形，因此可得E为CF的中点，即CE= CF.又有已知条件∠BDA=∠CDE知，∠ABD=∠ACF(等角的余角相等），进而易证△ABD≌△ACF，因此BD=CF，则结论得证。
略
WORD格式（
