如图1，在Rt△ABC中，∠C=90°，AC=4，BC=3．点P从点B出发，沿BA方向以每秒1个单位长度的速度向点A匀速运动；点Q从点A同时出发，沿AC方向以每秒2个单位长度的速度向点C匀速运动．连接PQ，设运动的时间为t（s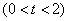），解答下列问题：

（1）当t为何值时，PQ∥BC？
（2）设△APQ的面积为y，求y与t之间的函数关系式；
（3）如图2，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻，
使四边形PQP′C为菱形？若存在，求出此时菱形的周长；若不存在，请说明理由．
（建议学生打印做题，并在做完之后对比解题思路中的示范照片）



1．当PQ∥BC时，t的值为(    )

• A.
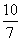
• B.
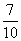
• C.
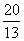
• D.

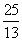
答案

正确答案：A

知识点：相似三角形的性质  动点问题  

见第6题中解析

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>