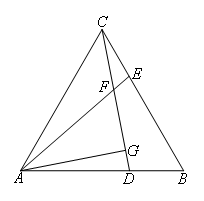
如图，在等边三角形ABC中，D，E分别在AB，BC边上，且AD=BE，AE与CD交于点F，
AG⊥CD于点G．下列结论：①AE=CD；②∠AFC=120°；③△ADF是等边三角形；④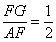．其中正确的结论是(    )

结论①：
在等边△ABC中，
AB=AC，∠BAC=∠B=60°，
又∵AD=BE
∴△ABE≌△CAD（SAS），
∴AE=CD，故①正确；
结论②：
由①知△ABE≌△CAD
∴∠ACD=∠BAE，
∴∠CAF+∠ACD=∠CAF+∠BAE=∠BAC=60°，
在△ACF中，∠AFC=180°-（∠CAF+∠ACD）=120°，
故②正确；
结论③：
∵∠FAD∠BAC，∠BAC=60°，
∴∠FAD≠60°，
∴△ADF不是等边三角形，故③错误；
结论④：
由②知∠AFC=120°
∴∠AFG=60°，
∵AG⊥CD，
∴∠FAG=30°，
在Rt△AFG中，∠FAG=30°，
∴，即，故④正确.
综上所述，正确的有①②④．
故选D

略