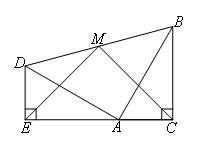
现有两个全等的含30°，60°角的三角板ADE和三角板ABC，按如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连接ME，MC．则∠MEC的度数为(    )

如图，连接AM．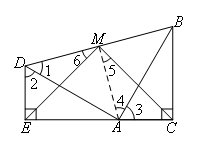

∵三角形ADE与三角形ABC是两个全等的含30°，
60°角的三角板，
∴∠2=∠3=60°，AD=AB，∠EAD=30°，DE=AC，
∴∠DAB=90°
∴△DAB为等腰直角三角形．
又∵M点为BD的中点，
∴AM⊥BD，∠1=45°，∠4=45°，AM=DM=BM，
∴∠EDM=∠CAM=45°+60°=105°
∴△DEM≌△ACM（SAS），
∴ME=MC，∠6=∠5，
∵∠AMD=90°，
∴∠6+∠EMA=90°，
∴∠5+∠EMA=90°，
即∠EMC=90°，
∴△MEC为等腰直角三角形，
∴∠MEC=45°．
故选C

略