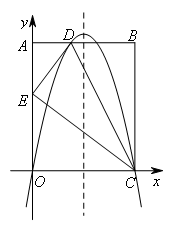
如图,在矩形OABC中,OA=10,AB=8,点D在AB边上,沿直线CD折叠,使点B落在OA边上的点E处.分别以OC,OA所在直线为x轴、y轴建立平面直角坐标系,抛物线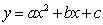 经过O,D,C三点.点N在抛物线对称轴上,点M在抛物线上,当以M,N,C,E为顶点的四边形是以CE为边的平行四边形时,点M的坐标为( )
经过O,D,C三点.点N在抛物线对称轴上,点M在抛物线上,当以M,N,C,E为顶点的四边形是以CE为边的平行四边形时,点M的坐标为( )
- A.
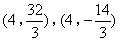
- B.
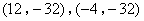
- C.
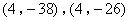
- D.
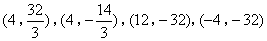
答案
正确答案:B
①整合信息,读题标注
易得O,C两点的坐标,要求过O,C,D三点的抛物线的解析式,只需求点D的坐标,进一步的只需求线段AD的长。
折叠转移边角关系,利用勾股定理建立等式求解AD.
可得抛物线的解析式为![]()
②分析特征,有序思考,设计方案;
分析定点、动点:C,E是定点,M,N为动点
确定分类标准:连接CE得到定线段,四个顶点用逗号隔开,位置不固定,题目中条件要求CE为边,故将定线段CE为边分析
③根据方案作出图形,有序操作
若CE为边,根据平行四边形的判定,则CE∥MN且CE=MN,要找MN,将线段CE拉出来,沿对称轴上下平移,确保点N在对称轴上,来找抛物线上的点M,找出点之后,设计方案,利用平移性质,求它们的坐标;
④检查验证
作图验证;分析数据,估算验证
2.解题过程
由折叠,BD=DE,CE=CB=10.
在Rt△COE中,OC=AB=8,CE=10,
∴OE=6,
∴AE=4.
设AD=m,则DE=BD=8-m,
在Rt△ADE中,由勾股定理可得![]() ,
,
解得![]() ,即
,即![]() ,
,
∴D(3,10).
∴抛物线的解析式为![]() ,且对称轴为直线x=4.
,且对称轴为直线x=4.
若以M,N,C,E为顶点的四边形是以CE为边的平行四边形,则MN∥CE,MN=CE,如图,

∵![]() ,且
,且![]() ,
,
∴![]() .
.
分别代入抛物线解析式可解得
![]() .
.
∴![]() ,
,![]() .
.
综上,满足题意的点M的坐标为![]() .
.
略








