将一副直角三角板如图放置,已知AE∥BC,则∠AFE的度数为( )
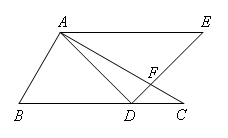
- A.95°
- B.100°
- C.110°
- D.105°
答案
正确答案:D
如图,
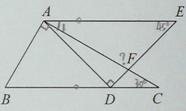
由题意可知,∠C=30°,∠E=45°,
因为AE∥BC,根据两直线平行,内错角相等,可得∠1=∠C=30°.
在△AEF中,∠1=30°,∠E=45°,由三角形的内角和等于180°,
可得∠AFE=180°-∠1-∠E=180°-30°-45°=105°.
故选D.
想一想:
1.我们学过的和余角、补角相关的定理分别是什么?自己尝试推理证明.
2.由角的关系得平行,可以考虑哪些定理?
3.由平行得角的关系,可以考虑哪些定理?
参考答案:
1.同角或等角的余角相等;同角或等角的补角相等.
已知∠1与∠2互余,∠1与∠3互余,
由互余可得∠1+∠2=90°,∠1+∠3=90°,
所以∠2=∠3,同角的余角相等;
已知∠1与∠2互余,∠3与∠4互余,∠2=∠3,
由互余可得∠1+∠2=90°,∠3+∠4=90°,
又因为∠2=∠3,所以∠1=∠4,等角的余角相等.
综上,同角或等角的余角相等.
可用类似的方法推理证明,同角或等角的补角相等.
2.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
3.两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
略








