问题情境:
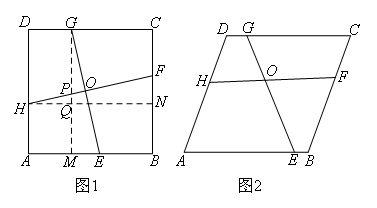
在特殊四边形的复习课上,老师出了这样一道题:如图2,在菱形ABCD中,E,F,G,H分别为AB,BC,
CD,DA边上的动点,连接EG,FH相交于点O,若∠HOE=∠D,试探究:EG与FH的数量关系.经过小组讨论后,小聪建议分以下两步进行:
(1)特殊情况,探索结论
当菱形ABCD是正方形时,如图1,EG与FH有怎样的数量关系呢?
小聪想:要求EG与FH的数量关系,就要构造全等三角形或相似三角形,于是,分别过点G,H作GM⊥AB于点M,HN⊥BC于点N,证明△GME≌△HNF,从而得到EG=FH.则判定△GME≌△HNF使用的条件可能是( )
- A.HL
- B.ASA或AAS
- C.SAS
- D.AAA
答案
正确答案:B


略








