如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,
∠DCE=15°,∠CEF=135°.求证:EF∥BC.
证明:如图,
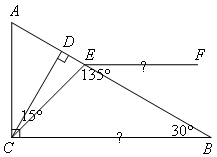
∵CD⊥AB(已知)∴∠CDB=90°(垂直的定义)
∵∠B=30°(已知)
∴∠DCB=90°-∠B=60°(直角三角形两锐角互余)
∴EF∥BC(同旁内角互补,两直线平行)
横线处应填写的过程最恰当的是( )
- A.

- B.

- C.

- D.

答案
正确答案:D
知识点:平行线的判定 直角三角形两锐角互余
本题条件比较多,首先读题标注,把思路走通.
在Rt△CDB中,利用直角三角形两锐角互余可得∠DCB=60°;
结合∠DCE=15°,可得∠ECB=45°;
因为∠CEF=135°,所以∠CEF+∠ECB=180°,因此可证EF∥BC.
故选D.
略









