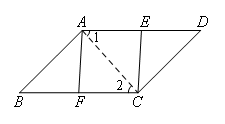
已知:如图,AB∥CD,AD∥BC,E,F分别是AD,BC的中点.
求证:AF=CE.

证明:如图,连接AC,
在△ABC和△CDA中

∴
∴BC=DA
在△AFC和△CEA中

∴
∴AF=CE
请你仔细观察下列序号所代表的内容:
①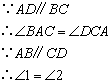 ;②
;②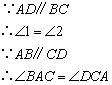 ;
;
③△ABC≌△CDA(ASA);④△ABC≌△CAD(AAS);
⑤ ;⑥
;⑥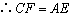 ;
;
⑦△CEA≌△CAF(SSA);⑧△AFC≌△CEA(SAS).
以上空缺处依次所填正确的是( )
- A.②④⑤⑦
- B.①③⑥⑧
- C.②③⑤⑧
- D.①④⑥⑦
答案
正确答案:C
要证AF=CE,考虑放在两个三角形中证全等,结合题中已知条件无法直接
证明AF和CE所在的三角形全等,因此考虑构造三角形,连接AC.
由两组平行可得∠1=∠2,∠BAC=∠DCA,AC是公共边,
由ASA可以证得△ABC≌△CDA,因此BC=DA.
由中点可知CF=AE,进而由SAS可以证得△AFC≌△CEA,因此AF=CE.
故选C.
略











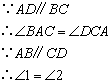 ;②
;②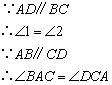 ;
; ;⑥
;⑥