如图，P为∠BAC内一点，PD⊥AB，PE⊥AC，垂足分别为D，E，且PD=PE．
求证：AD=AE．

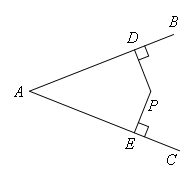
证明：如图，连接AP，

                        
在Rt△APD和Rt△APE中
                        
∴Rt△APD≌Rt△APE（     ）
∴AD=AE
请你仔细观察下列序号所代表的内容：
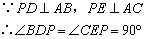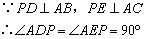①；②；③；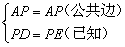
④；⑤SAS；⑥SSA；⑦HL．
以上空缺处依次所填正确的是(    )

• A.①④⑦
• B.②③⑦
• C.②④⑦
• D.②④⑤

答案

正确答案：B

知识点：全等三角形的性质与判定  与三角形全等有关的辅助线  

要证AD=AE，可以考虑放在两个三角形中证全等，连接AP构造三角形．
结合题中条件可知△APD和△APE都是直角三角形，
由HL可以证得Rt△APD≌Rt△APE，进而得到AD=AE．
故选B．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>