善于学习的小敏查资料知道：对应角相等，对应边成比例的两个梯形，叫做相似梯形．他想到“平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似”，提出如下两个问题．
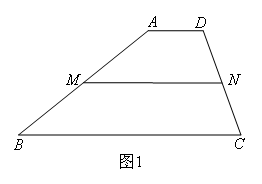
问题一：平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似？（1）从特殊情形入手探究．假设梯形ABCD中，AD∥BC，AB=6，BC=8，CD=4，AD=2，MN是中位线，如图1．根据相似梯形的定义，能够证明梯形AMND与梯形ABCD不相似；由此推广到一般结论：平行于梯形底边的直线截两腰所得的梯形与原梯形(    )

• A.相似
• B.不相似
• C.相似性无法确定

答案

正确答案：B

知识点：相似之类比探究  相似图形的判定  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>