在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
求证:DE=AD+BE.

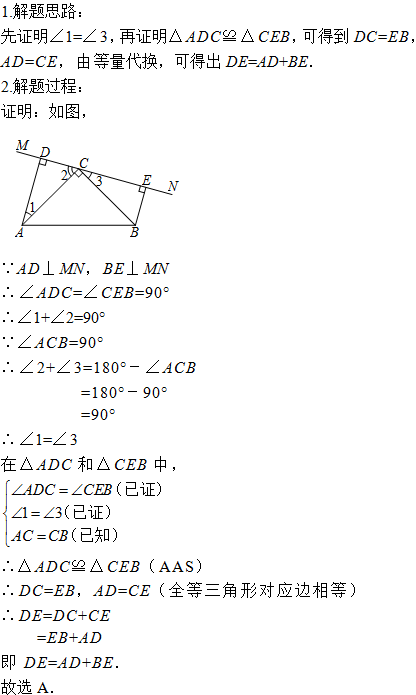
证明:如图,

∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
∴∠1+∠2=90°
∵∠ACB=90°
在△ADC和△CEB中
∴△ADC≌△CEB(AAS)
即DE=AD+BE.
① ;②
;② ;③
;③ ;
;
④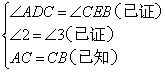 ;⑤
;⑤ ;
;
⑥
以上空缺处依次所填最恰当的是( )
- A.①③⑥
- B.①④⑤
- C.②④⑥
- D.②③⑤
答案
正确答案:A
知识点:全等三角形的判定与性质
略









 ;②
;② ;③
;③ ;
;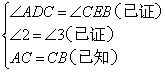 ;⑤
;⑤
