已知，如图，AB∥CD，E是AC上一点，∠B=30°，∠D=60°．求证：BE⊥ED．

证明：如图，

                    
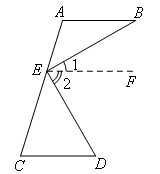
∴∠B=∠1，∠D=∠2
∵∠B=30°，∠D=60°
∴∠1=30°，∠2=60°
∴∠BED=∠1+∠2 
       =30°+60°
       =90°
即：BE⊥ED
以上空缺处所填正确的是(    )

• A.
  ∵AB∥CD
  ∴AB∥EF∥CD
• B.
  过点E作EF∥AB
  ∵AB∥CD
  ∴AB∥EF∥CD
• C.
  过点E作AB∥EF∥CD
• D.
  过点E作EF∥AB
  ∴AB∥EF∥CD

答案

正确答案：B

知识点：平行线的性质  与角有关的辅助线  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>