如图,在平面直角坐标系中,O是坐标原点,四边形AOCD是含有60°角的菱形,顶点A的坐标为(-4,0),边AO在x轴上,点E为线段AD的中点,点F在线段CD上,且横坐标为1,直线EF与y轴交于点G,有一动点P从点A以每秒2个单位长度的速度沿折线A→O→C→F运动,当点P到达点F时停止运动,设点P运动时间为t秒.

(1)直线EF的表达式为( )
- A.
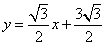
- B.
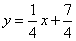
- C.
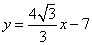
- D.
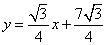
答案
正确答案:D
知识点:待定系数法求一次函数解析式 动点问题
1.解题要点
①研究背景图形,将信息标注在图形上.
如图,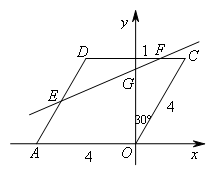
四边形AOCD是含有60°角的菱形,A(-4,0),可得![]() ,
,![]() ,
,
∵E是AD的中点,
∴![]() .
.
∵点F的横坐标为1,
∴![]() .
.
②分析运动过程,分段定范围.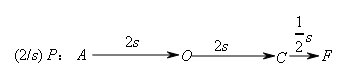
∴![]() .
.
③分析几何特征、表达、设计方案求解.
根据点E,F的坐标,利用待定系数法可得直线EF的表达式.
2.解题过程
∵四边形AOCD是含有60°角的菱形,![]() ,
,
∴![]() ,
,![]() .
.
∵E是AD的中点,
∴![]() .
.
∵点F的横坐标为1,
∴![]() .
.
设直线EF的表达式为![]() ,
,
∴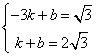 ,解得
,解得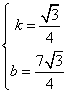 ,
,
∴![]() .
.
故选D.
略








