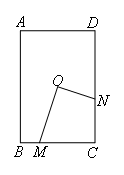
如图，O为矩形ABCD的中心，M为BC边上任一点，ON⊥OM且与CD边交于点N．
若AB=6，AD=4，设OM=x，ON=y，则y与x之间的函数关系式为( )
- A.
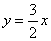
- B.
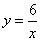
- C.
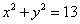
- D.
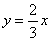
答案
正确答案：D
知识点：矩形的性质 相似三角形的性质及判定 斜直角的处理思路
如图，过点O作OE⊥CD于点E，OF⊥BC于点F，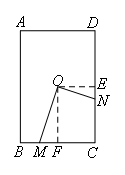
在矩形ABCD中，AB=6，AD=4，点O为矩形ABCD的中心，
∴OE=2，OF=3，∠C=90°．
∵OE⊥CD，OF⊥BC，
∴∠OFM=∠OEN=90°，四边形OECF为矩形，
∴∠EOF=90°．
∵ON⊥OM，
∴∠NOM=90°，
∴∠FOM=∠EON．
∴△OFM∽△OEN．
∴
．
∵OM=x，ON=y，
∴
，即．
故选D．
略
WORD格式（
