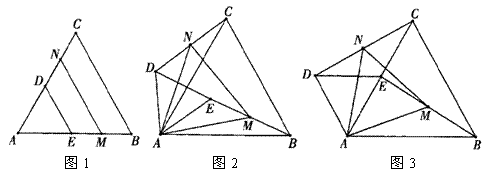
(2009湖南常德)如图1,若△ABC和△ADE为等边三角形,M,N分别是EB,CD的中点,易证:CD=BE,△AMN是等边三角形.(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明,并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比;若不是,请说明理由.
答案
答:(1)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∵∠BAE=∠BAC-∠EAC=60°-∠EAC,∠DAC=∠DAE-∠EAC=60°-∠EAC,
∴∠BAE=∠DAC,∴CD=BE.
(2)△AMN是等边三角形.理由如下:
∵△ABE≌△ACD,M、N分别是BE、CN的中点,
∴AM=AN,NC=MB.
∵AB=AC,
∴△ABM≌△ACN,
∴∠MAB=∠NAC,
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°,
∴△AMN是等边三角形,
设AD=a,则AD=AE=DE=a,AB=BC=AC=2a,易证BE⊥AC,
∴![]() ,
,
∴![]() ,
,
∴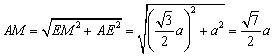 ,
,
∵△ADE,△ABC,△AMN为等边三角形,
∴![]() .
.
知识点:中考压轴之实践操作、问题探究
(1)利用SAS判定△ABE≌△ACD,全等三角形的对应边相等,所以CD=BE.
(2)证明△AMN是等边三角形,AD=a,则AB=2a,根据已知条件分别求得△AMN的边长,因为△ADE,△ABC,△AMN为等边三角形,所以面积比等于边长的平方的比.
略








